前言

堆排序是以堆为原型的排序。堆首先是一棵二叉树，具有以下两个性质：每个节点的值大于或者等于其左右孩子结点的值，称为大顶堆；或者每个节点的值都小于或者等于其左右孩子结点的值，称为小顶堆。从这个定义中可以发现，堆得根节点要么是最大值要么是最小值。实现堆排序的基本思想是：将待排序的序列构造成一个大顶堆或者小顶堆。此时整个堆满足根节点是最大值或者最小值。将根节点移走，并与堆数组的最后一个值进行交换，这样的话最后一个值就是最大值或者最小值了。然后将剩余n-1（假设原来总共有n个元素）未排序的序列重新构造成一个最大堆或者最小堆，再与除原来最大值之外的最后一个元素进行交换，得到次小值。如此反复进行，就得到一个排序的序列。

堆排序算法的Java实现

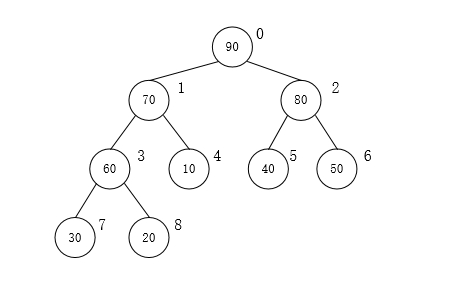
package com.rhwayfun.algorithm.sort;public class HeapSort2 {    public void heapSort(int[] a){        for(int i = a.length/2-1; i >= 0; i--){            //建立一个最大堆            heapAdjust(a,i,a.length - 1);        }        for (int i = a.length - 1; i > 0; i--) {            //将堆顶元素与当前未经排序的最后一个记录交换            swap(a,0,i);            //将数组a中下标从0到i-1的子序列重新调整为最大堆            heapAdjust(a, 0, i - 1);        }        for (int i = 0; i < a.length; i++) {            System.out.println(a[i]);        }    }    private void swap(int[] a, int i, int j) {        int temp = a[i];        a[i] = a[j];        a[j] = temp;    }    private void heapAdjust(int[] a, int s, int m) {        int temp = 0,j=0;        //把堆顶元素保存在临时变量中        temp = a[s];        //由于s可能是0，所以需要+1。此外，如果当前结点的序号是s，那么其左孩子是2*s+1(+1是因为s可能是0)        for(j = 2*s+1; j <= m; j = 2*j+1){            //找出左右孩子较大的结点的下标            if(j < m && a[j] < a[j+1]){                ++j;            }            if(temp >= a[j]){                break;            }            //把较大的孩子结点的赋给当前结点            a[s] = a[j];            //把更大孩子结点的下标赋给s            s = j;        }        //把原来s下标位置的值赋给新的下标为s的值，这样就完成了当前结点与更大孩子结点值的交换        a[s] = temp;    }    public static void main(String[] args) {        new HeapSort2().heapSort(new int[]{
    90,70,80,60,10,40,50,30,20});    }}

可以发现在建立最大堆的时候，i是从a.length/2开始的，为什么要从这个位置开始呢？比如有一个数组{

一共有9个元素，那么a.length/2−1的值是3，也就是第4个元素，执行for循环，i的值从3->2->1->0变化,可以发现这几个下标的结点都是有孩子结点的元素，所以第一个for循环就很好理解了：其实就是从下往上、从右到左，将每个非终端结点当做根节点，将其和子树调整成最大堆，所以下标3->2->1->0的变化，也就是60，80，70，90结点的调整过程。

堆排序算法的时间复杂度

可以发现堆排序的主要时间主要花在建堆和重建堆时的反复筛选上。在初始建堆的时候，由于只涉及两个节点的交换操作，所以建堆的时间复杂度是O(n)。在正式排序的时候，第i次取堆顶的元素并重建堆需要花去O(logi)的时间，需要n-1次取堆顶记录，所以排序的过程的时间复杂度是O(nlogn)。而且这是最好、最坏和平均的时间复杂度，但是由于记录的交换与比较是跳跃式的，所以与归并排序不同，堆排序是一种不稳定的排序算法。

由于初始建堆的比较次数比较多，所以堆排序不适合记录数较少的情况（使用简单排序算法是一种不错的选择，没必要大材小用了）。